
БИНОМ НЬЮТОНА
ИСТОРИЯ БИНОМА НЬЮТОНА
Евклид
III в. до н.э.
Рассматривал биномиальное разложение для n, равного 2: (а + b) = a + 2ab + b
2
2
2
Источник
Биномиальное разложение
Малых А.Е. Из истории биномиальной теоремы / – А.Е. Малых – Текст: непосредственный // Ярославский педагогический вестник. – 2010. – № 3. – С. 25.

Страна
Название работы
Название формулы
"Начала"
Древняя Греция
Брахмагупта
598-626 гг.
Утверждал, что "Сумма квадратов есть сумма чисел, умноженная на удвоенное число шагов, увеличенное на единицу, и делённая на три. Сумма кубов есть квадрат суммы чисел до одного и того же числа". Однако, доказательство не приводил.
Страна
Название работы
Индия
Название формулы
Сумма квадратов и кубов
Источник
Первоисточник - Plofker K. Mathematics in India // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A sourcebook / Editor Katz V. J.. — Princeton University Press, 2007. — 685 p, p. 428—434
"Брахма-спхута-сиддханта" ("Пересмотр системы Брахмы")

Цзя Сянь
1010-1070 гг.
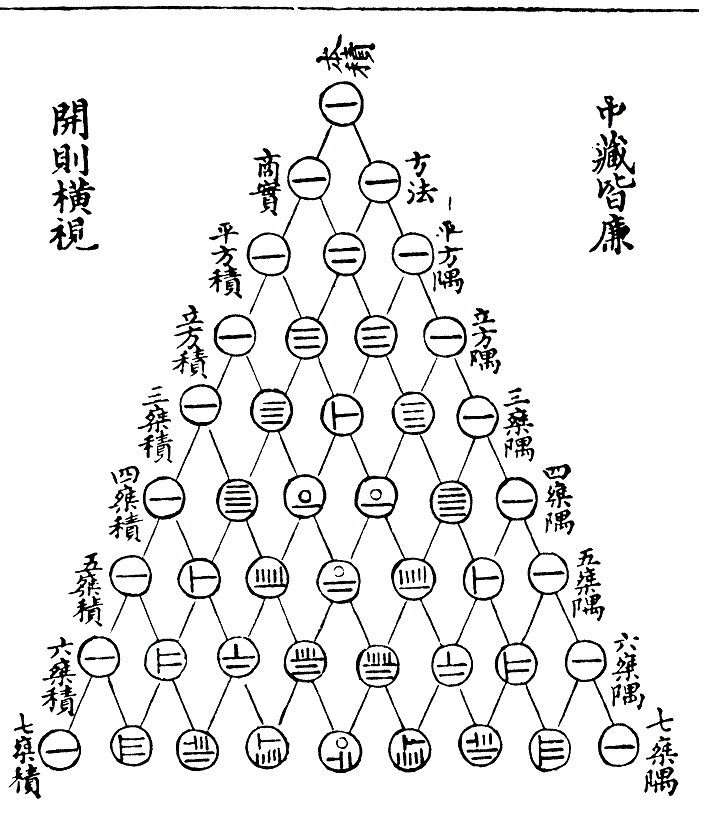
Составил треугольную таблицу биномиальных коэффициентов до n = 6.
Использовал его как инструмент для извлечения квадратного и кубического корня.
Страна
Китай
Название работы
"Методы счета Хуан-ди в девяти главах с подробными решениями"
Название формулы
Биномиальные коэффициенты ("Треугольник Цзя Сяня")
Источник

Ян Хуэй
1261 г.
Описал метод нахождения квадратных и кубических корней с использованием "Треугольника Цзя Сяня".
Страна
Китай
Название работы
"Сянцзе Цзючжан Суанфа"("Подробное разъяснение методов исчисления в девяти разделах")
Название формулы
Квадратные и кубические корни
Источник

Насир ад-Дин Туси
1265 г.
Описал приём извлечения корней из любой степени.
Привел таблицу биномиальных коэффициентов.
Страна
Персия (Ирак)
Название работы
"Сборник по арифметике с помощью доски и пыли"
Название формулы
Биномиальные коэффициенты
Источник
Статья - с. 8-12.


Чжу Шицзе
1303 г.
Находил квадратные и кубические корни, привел коэффициенты, сейчас известные как коэффициенты треугольника Паскаля. Но автором метода указал Цзя Сяня.
Страна
Китай
Название работы
Название формулы
Биномиальные коэффициенты
Источник

Аль-Каши
1427 г.
Изложил приемы извлечения корней любой степени, один из которых был основан на применении формулы, известной сейчас как бином Ньютона.
Страна
Название работы
Название формулы
Источник
Персия (Иран)
Извлечение корней любой степени

Михаэль Штифель
1544 г.
Составил таблицу биномиальных коэффициентов до 18-ой степени.
Страна
Германия
Название работы
"Arithmetika integra" ("Обобщенная арифметика")
Название формулы
Извлечение корней любой степени
Источник

Никколо Тарталья
1556-1560 гг.
В своем труде расположил коэффициенты разложения степени бинома вдоль диагонали, соединяющей соответствующие номера строк и столбцов. Треугольник, отсеченный такой диагональю, впоследствии стал известен как треугольника Паскаля.
Страна
Италия
Название работы
"Общий трактат о числе и мере"
Название формулы
Прообраз треугольника Паскаля
Источник
Малых А.Е. Из истории биномиальной теоремы / – А.Е. Малых – Текст: непосредственный // Ярославский педагогический вестник. – 2010. – № 3. – С. 27.

Рафаэль Бомбелли
1560 г.
В своем труде привел разложение бинома до n = 7, используя коэффициенты при вычислении соответствующих корней.
Страна
Италия
Название работы
"Алгебра"
Название формулы
Разложение бинома
Источник
Малых А.Е. Из истории биномиальной теоремы / – А.Е. Малых – Текст: непосредственный // Ярославский педагогический вестник. – 2010. – № 3. – С. 27.

Джероламо Кардано
1570 г.
Основываясь на трудах Штифеля ввел биномиальные коэффициенты.
Страна
Италия
Название работы
"Новом труде о пропорциональностях"
Название формулы
Биномиальные коэффициенты
Источник
Майстров, Л.Е. Теория вероятностей: исторический очерк / Л.Е. Майстров ; отв. ред. И.Б. Погребысский ; Академия наук СССР, Институт истории естествознания и техники. – Москва : Наука, 1967. – С.30
Иоганн Фаульгабер
1617 г.
Привел без доказательства значения для суммы степеней m первых восьми чисел натурального ряда.
Страна
Германия
Название работы
"Продолжение нового чудесного искусства"
Название формулы
Биномиальные коэффициенты
Источник
Малых А.Е. Из истории биномиальной теоремы / – А.Е. Малых – Текст: непосредственный // Ярославский педагогический вестник. – 2010. – № 3. – С. 27.

Блез Паскаль
1654 г.
Описал треугольную таблицу, позволяющую находить биномиальные коэффициенты, названную впоследствии его именем. Строго описал и привел доказательства такого способа.
Страна
Франция
Название работы
"Трактате об арифметическом треугольнике"
Название формулы
Биномиальные коэффициенты ("Треугольник Паскаля")
Источник

Исаак Ньютон
1665-1669 гг.
На основании трудов предшественников вывел формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменны, впоследствии названной - Бином Ньютона.
Страна
Великобритания
Название работы
«Анализ с помощью уравнений с бесконечным числом членов»
Название формулы
Биномиальное разложение ("Бином Ньютона")
Источник

Джеймс Грегори
1670 г.
В письме к Коллинсу от 23 ноября 1670 г. видно, что Грегори владел в 1670 общим разложением бинома. Т.е. открыл независимо от Ньютона.
Страна
Великобритания
Название работы
- (письмо)
Название формулы
Биномиальное разложение ("Бином Ньютона")
Источник
Юшкевич А.П. История математики с древнейших времен до начала XIX столетия. Том 2 / А.П. Юшкевич – Рипол Классик, 2013 – С. 165.

Якоб Бернулли
1713 г. издания
В своем труде ввел "числа Бернулли", отталкиваясь от соотношений биномиальных коэффициентов.
Страна
Название работы
Название формулы
Источник
Швейцария
«Искусство предположений» (Ars conjectandi)
Биномиальные коэффициенты
ИНТЕРАКТИВНАЯ КАРТА
ПОЧЕМУ ФОРМУЛА БИНОМА НОСИТ ИМЯ И. НЬЮТОНА?
Что такое Формула Бинома? Это двучлен n-ной степени. С такой формулой работали математики еще до И. Ньютона. До И. Ньютона было открыто двучлен натуральнй степени. Но именно И. Ньютон обобщил эту формулу для дробной и отрицательной степени. В результате, он получил полную обобщенную формулу на основании выводов древних математиков.
ВЕРНО ЛИ ИСТОРИЧЕСКИ НАЗВАНИЕ «БИНОМ НЬЮТОНА»?
Название формулы Бином Ньютона не является исторически справедливым, так как ученые до Ньютона знали эту формулу. Несомненно, следует отметить, что именно благодаря И. Ньютону эта формула получила широкую известность.
ПОЧЕМУ В РАЗНЫХ СТРАНАХ МИРА ФОРМУЛУ БИНОМА НЬЮТОНА НАЗЫВАЮТ ПО-РАЗНОМУ?
В работах разных ученых Бином Ньютона называется по-разному потому, что каждый из ученых считал эту формулу достоянием своей страны, также не было единого обобщенного вида бинома. Поэтому ученые, изучавшие бином Ньютона до самого Ньютона, не могли сравнить свои работы и определить их принадлежность к одной и той же формуле.
В результате, в разных странах мира ее называют по-разному: биномиальной теоремой, биномиальным распределением, формулой числа сочетаний.
ПРИМЕНЕНИЕ ФОРМУЛЫ БИНОМА НЬЮТОНА
Бином Ньютона – фундаментальная формула математики. С ее помощью можно вести расчеты, которые раньше считались непостижимыми. Естественно, что она получила широкое распространение при решении различных задач.
Даже классики литературы в своих произведениях и режиссеры киноискусства в фильмах (казалось бы, далекие от математики) употребляли выражение «бином Ньютона». Приведу примеры: роман «Последнее дело Холмса» А.К. Дойла, повесть «Юность» Л.Н. Толстого, роман «Мы» Е.И. Замятина, роман «Мастер и Маргарита» М.А. Булгакова, фильм «Сталкер» А.А. Тарковского.
Самое широкое применение бином Ньютона получил, конечно же, в математике. Школьный курс алгебры знакомит нас с формулами сокращенного умножения. Квадрат суммы двух выражений, квадрат разности двух выражений, куб суммы двух выражений, куб разности – есть ни что иное, как применение формулы бинома Ньютона для второй и третьей степени двучлена.
Мы знаем наизусть эти формулы. Но если увеличивать показатель степени, то начнутся определенные трудности. Поэтому для возведения в степень двучлена применяют обобщенную формулу бинома Ньютона для натуральных степеней.
В математике бином Ньютона используется при решении задач на делимость, сокращении дробей, в приближенных вычислениях.
Пример 1. Доказать, что число 11 — 1 делится на 100.
Решение.
Преобразовав данное выражение с помощью бинома Ньютона, выяснили, что один из множителей многочлена делится на 100. Можно утверждать, что все выражение делится на 100.
10

Пример 2. Использование бинома Ньютона для приближенных вычислений.
Пусть а = 1, b = х, получим:
Придадим величине х малое значение. Тогда значения величин х, х, ..., х также будут небольшими. Отбросим в формуле (1) члены, содержащие х, х, ..., х. В результате получим приближенную формулу
Ошибка такого приближения будет небольшой. Так как C = n, то формулу можно переписать в виде:
Рассмотрим на конкретном примере: х=0,01
При n = 2 (1 + 0,01) ≈ 1, 02
При n = 3 (1 + 0,01) ≈ 1, 03
Формула (2) верна и для малых отрицательных значений х.
Помимо приведенных примеров, Бином Ньютона применяют при доказательстве различных теорем: теоремы Ферма, выводе формулы Ньютона-Лейбница, в теории бесконечных рядов.
2
3
n
2
3
n
1
n
2
3